Linear Algebra

Linear Algebra is like the language of data science. It helps us describe, manipulate, and understand data, especially when the data is structured in tables, grids, or images.

Basics

1. Scalars, Vectors, Matrices, and Tensors
   • Scalars: Just a single number. Imagine the weight of a watermelon: 5 kg. That’s a scalar.
     • A scalar is a single number, like a=5. Scalars are used to represent single measurements or constants.
   • Vectors: A vector is an ordered list of numbers, represented as:

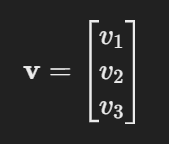
1. For example, the position of a point in a 3D space might be represented as:

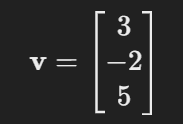
Learn Scalars and Vectors in-depth

• Matrices: A matrix is a grid of numbers, such as:

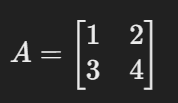
Matrices are used to represent datasets, transformations, or systems of equations.

Learn Matrices in-depth

• Tensors: Tensors are higher-dimensional arrays. For instance, a color image can be represented as a 3D tensor, where each layer represents a color channel (Red, Green, Blue).

Learn Tensors in-depth

• Matrix Operations
  • Addition: Adding matrices is like combining two layers of the same table.
    Example: Adding sales from two different stores.

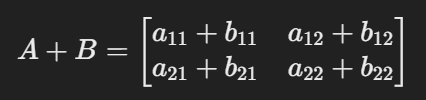
• Multiplication: This is used to combine information.
  Example: You have a matrix of fruit prices and a matrix of quantities sold—multiplication helps calculate total revenue.

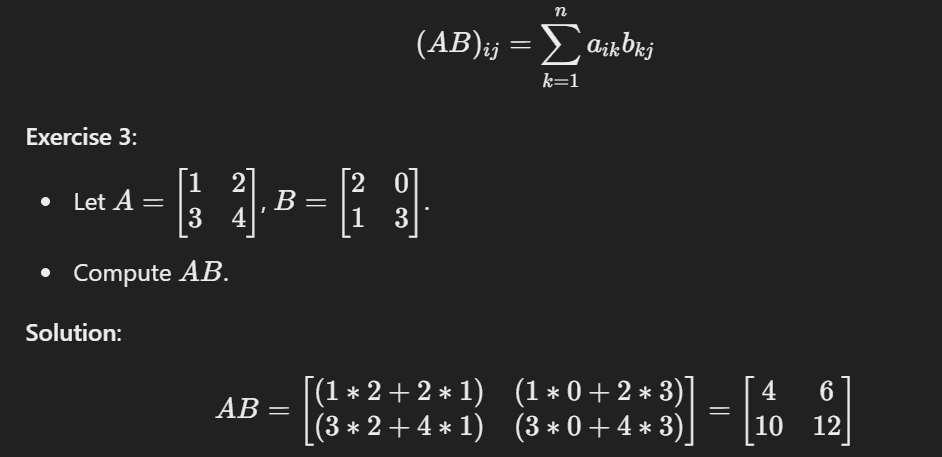
• Transposition: Flipping rows into columns. Useful for organizing data.

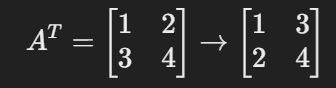
Key Concepts for Data Science

• Dot Product and Matrix Multiplication
  • The dot product helps measure similarity.
    Example: If you’re comparing two playlists, the dot product tells you how similar their song preferences are.

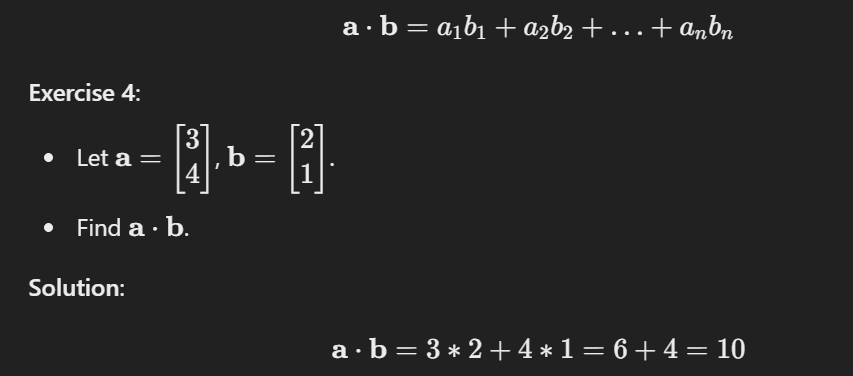
• Matrix Multiplication helps in applying transformations to data.
  Example: Rotating an image or scaling a graph.
• Determinants and Inverses
  • Determinants: Help us understand whether a matrix (and the system it represents) is solvable.
    Real-world analogy: Checking if a puzzle has a solution.
  • Inverses: The matrix equivalent of dividing numbers.
    Example: If you know the output and want to find the input, inverses help reverse the operation.
• Eigenvalues and Eigenvectors
  These are like the DNA of a matrix, showing its most important features.
  • Eigenvectors: Indicate the directions where data varies the most.
  • Eigenvalues: Tell us how significant that variation is.
    Example: In facial recognition, eigenvalues and eigenvectors help identify unique features of a face.

Applications in Data Science

1. Dimensionality Reduction (PCA Overview)
   Imagine a giant spreadsheet with 1000 columns of data. It’s overwhelming to analyze, right? Principal Component Analysis (PCA) simplifies it by finding the most important patterns and reducing the number of columns while keeping the essence of the data.
   Example: Analyzing customer preferences across thousands of products by focusing on key categories.
2. Vectorized Operations in Machine Learning
   When training machine learning models, we often perform calculations on millions of numbers at once. Linear algebra makes this efficient by handling entire datasets (matrices) at once instead of one number at a time.
   Example: Training an image recognition model involves multiplying matrices representing pixel intensities and weights.

Linear Algebra forms the building blocks of many data science techniques, from transforming data to making algorithms run faster. Understanding these basics will empower you to unlock the full potential of data science tools.